Settantasette milioni di euro di jackpot, eppure la strategia migliore è quella di non giocare. Oppure finali al cardiopalma con premi da capogiro che fanno riflettere su quanto valga la pena di proseguire ad aprire pacchi, eppure il metodo per aggiudicarsi più soldi possibili rimane spesso quello di ignorare le offerte del dottore ed accettare il cambio solo in condizioni particolari. Dalle scommesse calcistiche fino al Superenalotto e persino a programmi di successo come Affari tuoi, la matematica si conferma l’unica variabile da non ignorare se non si vuole correre il rischio di cadere in tranelli realizzati da chi semplicemente il gioco l’ha pensato e costruito. Nonostante l’impulso emotivo di scegliere determinati numeri in base a sogni, premonizioni, date di nascita o di anniversario, è possibile dimostrare statisticamente che l’unica cosa che conta davvero è fermarsi, respirare e fare i conti, i quali mostrano che la strategia migliore è quella di non giocare nel caso delle scommesse e di non accettare offerte significativamente inferiori al valor medio, preferendo piuttosto il cambio solo se i pacchi di basso valore (i pacchi blu) risultano numericamente inferiori di quelli di alto valore (i pacchi rossi) nel caso di Affari tuoi.

Il concetto di Valore atteso

Per comprendere i meccanismi che regolano la maggior parte dei giochi d’azzardo, risulta fondamentale il concetto di “valore atteso” di una variabile aleatoria, chiamato anche “media” o “speranza matematica”. Tale quantità non è altro che la media dei valori possibili pesati rispettivamente con la loro probabilità di essere assunti. Si calcola similmente ad una media aritmetica pesata (si pensi per esempio a voti di scuola dal valore diverso), con l’unica differenza che il peso è dato dalla probabilità dell’evento. Considerando per esempio il lancio di una moneta equa che aggiudica il punteggio +1 per ogni testa e 0 per ogni croce, il valore atteso in un lancio sarà 0,5, mentre sarà 5 in 10 lanci e 25 nel caso vengano effettuati 50 lanci. Considerando un dado equo con sei facce e aggiudicando punteggi uguali al valore del lato estratto (+1 se esce 1, +2 se esce 2 e così via…), è facile accorgersi che “mediamente” ad ogni lancio ci si aspetta di ottenere 3,5, in quanto la somma dei 6 valori, ognuno moltiplicato per la probabilità di essere assunto (1/6) è proprio 3,5.

La matematica del Superenalotto

Usando questo semplice concetto non è difficile dimostrare che nel caso del Superenalotto – così come in tutti gli altri casi di scommesse dove le quote vengono appositamente regolate in maniera simile – la strategia migliore per vincere soldi è sempre quella di non giocare. Per comprenderne meglio i meccanismi, si può partire da due esempi che forniscono tutti gli elementi matematici che possono poi essere estesi al Superenalotto. Si immagini di scommettere 1 euro su un gioco che prevede il lancio di moneta equa che raddoppia l’importo nel caso di vincita (si supponga testa) e prevede invece la perdita della somma scommessa nel caso opposto (si supponga croce). In questo caso si tratta di un caso perfettamente bilanciato dove il giocatore vince mediamente un euro per ogni euro speso (ovvero mediamente non vince niente). Infatti, il valore medio risulta essere uguale a 1 moltiplicato per 0,5 (l’euro guadagnato moltiplicato per la probabilità dell’evento), a cui va sommato -1 moltiplicato per 0,5 (l’euro speso per giocare che viene perso, moltiplicato per la probabilità di perdita). Sommando si ottiene 0,5 – 0,5, che fa 0. Si supponga invece di partecipare ad un gioco che prevede la scommessa di un euro su quale tra 3 scatole contenga due euro, che vengono vinti nel caso di scelta corretta. Applicando lo stesso principio, non è difficile mostrare che in questo caso per ogni euro giocato vengono attesi 66,6 centesimi di vincita, il che equivale a dire che ad ogni tentativo corrisponde una perdita media di 33,3 centesimi. Infatti, la vincita media risulta essere uguale a 1 moltiplicato per un terzo (l’euro guadagnato moltiplicato per la probabilità di vittoria), a cui bisogna sommare due volte i casi di perdita, che prevedono ciascuno -1 moltiplicato per un terzo. La media risulterà quindi uguale a 1*1/3 + (-1)*1/3 + (-1)*1/3, che infatti fa circa -0,333 (ovvero -33,3 centesimi).

È facile mostrare quindi che per creare una scommessa svantaggiosa per il giocatore e favorevole al banco basta stabilire una vincita la quale assicuri comunque che lo sfidante perda mediamente denaro ad ogni tentativo. È lo stesso principio sfruttato dalla roulette dei casinò (che infatti paga 36 volte la somma scommessa su un numero che però ha probabilità 1/37 di essere scelto) e persino dal Superenalotto: al momento della stesura di questo articolo la quota jackpot assicurata nel caso di 6 punti risulta essere pari a 77.000.000€. Si tratta di una cifra esorbitante e che anche per questo può trarre in inganno, ma che è in realtà irrisoria se si pensa alla probabilità di estrarre effettivamente tutti e 6 i numeri fortunati, che è di 1/622.614.630. Lo stesso si può dire per i 5 punti, che pagano circa 32.000€ nonostante la probabilità di ottenerli sia una su oltre un milione e così via. Sviluppando i calcoli risulta che, mediamente, ogni euro giocato corrisponde ad una vincita inferiore ai 50 centesimi, da cui consegue che la cosa più conveniente da fare è non giocare.

La matematica di Affari tuoi ed il problema di Monty Hall

Per quanto riguarda il famoso programma televisivo Affari tuoi, la sfida prevede 20 pacchi di diverso valore, di cui la metà corrispondente ad una vincita inferiore ai 500 euro (i cosiddetti “pacchi blu”) e l’altra metà corrispondente a somme che vanno dai 5 a 300 mila euro (i cosiddetti “pacchi rossi”). Di questi, solo uno viene assegnato al giocatore, il quale durante il gioco dovrà scegliere quali scartare, sperando chiaramente di tenere per ultimi quelli dal valore maggiore e di ritrovarsi quindi con un pacco vincente. Durante l’apertura però, entra in scena il Dottore, che può decidere di proporre al giocatore di terminare il gioco in cambio di un’offerta o di sostituire il pacco con un altro tra quelli ancora in gioco. Dal punto di vista prettamente teorico e assumendo come unico obiettivo quello di assicurarsi la maggiore possibilità di vincere più denaro possibile, la strategia statisticamente migliore è quella di rifiutare qualsiasi offerta al di sotto del valor medio e di accettare il cambio solo in determinate situazioni che aumenterebbero la probabilità di vittoria.

Per quanto riguarda le offerte del Dottore quindi, basta calcolare direttamente la media probabilistica dei pacchi rimasti e valutare se la quota proposta è inferiore o maggiore. Per esempio, nel caso in cui i pacchi rimasti siano del valore di 0€, 1.000€, 20.000€ e 100.000€, il valore medio del pacco del concorrente (così come quello degli altri 3 pacchi in gara) sarebbe di 30.250€, il che significherebbe che le proposte inferiori a tale quota andrebbero teoricamente rifiutate. Tuttavia, osservando diverse puntate non sarà difficile accorgersi che le offerte del dottore sono spesso significativamente inferiori al valor medio in gioco. Il motivo però si basa presumibilmente sul fatto che, essendo un programma televisivo, le offerte devono garantire spettacolarità e suspense, giocando inoltre sul fatto che il concorrente non è una macchina ma un essere umano per cui, per i più svariati motivi, può risultare più comoda una somma garantita piuttosto che rischiare di tornare a casa a mani vuote.

Ma se le offerte possono essere più o meno discutibili in quanto suscettibili a motivi privati ed a bisogni economici, la scelta di cambiare o meno il pacco è prettamente teorica e probabilistica, e quindi determinata dall’avanzamento del gioco. Per capire quando è vantaggioso scambiare o meno il proprio pacco, può essere utile ragionare su un famoso quesito chiamato Problema di Monty Hall: si supponga di partecipare ad un programma televisivo dove sono presenti tre porte, di cui una contenente una lussuosa auto sportiva e due contenenti una capra. Al concorrente viene chiesto di scegliere una porta e, in seguito alla decisione, il conduttore apre una delle due contenenti una capra. Rimangono quindi due porte, di cui una contenente una capra e una l’auto, delle quali una chiaramente è stata scelta dal concorrente. Il conduttore decide così di proporre di scambiare la porta scelta inizialmente con la porta rimasta e lo scopo del quesito è capire quale sarebbe la scelta più conveniente e perché.

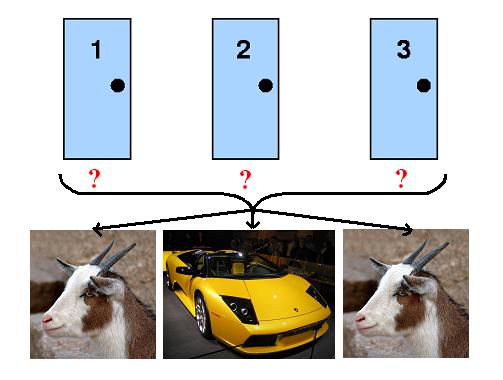
Nonostante possa risultare controintuitivo, la soluzione consiste nel scegliere di accettare il cambio, in modo da migliorare le proprie possibilità di vittoria dal 33,3% iniziale al 66,6%. Accettando lo scambio, infatti, è come se si stesse scommettendo sul fatto che la scelta iniziale sia stata perdente (che succede in due casi su tre) e che tale scelta venga sostituita in seguito con quella vincente. Se la spiegazione non dovesse bastare, può essere utile pensare a tutti i casi possibili: supponendo che l’auto si nasconda dietro alla seconda porta, rifiutando lo scambio la probabilità di vincita rimarrebbe sempre di 1/3, mentre accettando può succedere che:

• Caso a) il concorrente sceglie la porta 1, il conduttore apre la 3, viene accettato lo scambio e vinta la macchina
• Caso b) il concorrente sceglie la porta 2, il conduttore apre la 3, viene accettato lo scambio e viene persa la macchina (il concorrente riceve la porta 1 contenente la capra)
• Caso c) il concorrente sceglie la porta 3, il conduttore apre la 2, viene accettato lo scambio e viene vinta la macchina

In due casi su tre quindi, accettando lo scambio si riceve la porta sperata e si vince il premio.

Applicando lo stesso principio ad Affari tuoi quindi, la regola per aumentare la probabilità di concludere la gara vincendo una quantità elevata di denaro è decidere di scambiare il proprio pacco soltanto se il numero dei pacchi blu in gioco risulta inferiore a quello dei rossi, assicurandosi così la speranza massima di vittoria.

[di Roberto Demaio]