Insiemi infiniti più grandi di altri in quanto contengono un’infinità “più potente” di elementi in più: ciò che può sembrare uno scioglilingua controintuitivo non è altro che pura matematica, anche se a riguardo esistono delle questioni ancora irrisolte che sembrano destinate a tormentare i più grandi pensatori almeno per decenni, se non per sempre come pensano alcuni filosofi. Nonostante i numeri naturali (0, 1, 2…), interi, razionali (le frazioni) e reali siano tutti insiemi con un’infinità di elementi, è possibile dimostrare che i primi tre contengono in realtà la stessa quantità, detta “numerabile”, mentre aggiungendo le radici ed i numeri trascendenti (come il famosissimo Pi greco) si ottiene un infinito “superiore”, detto “del continuo”. Sorge spontaneo chiedersi allora se esistano o meno dei “livelli intermedi”, ovvero degli insiemi che contengono più elementi dei numeri naturali ma meno dei reali, e la cosa sorprendente è che la risposta a questo dilemma non la sappiamo, o meglio, non possiamo dimostrarla e forse non riusciremo mai a farlo. Ancora oggi e dopo millenni quindi, l’infinito e la teoria degli insiemi si confermano tra le aree di indagine più avvincenti in assoluto in quanto uniscono matematica e filosofia ed insegnano all’essere umano che, molto probabilmente, non scoprirà mai la ragione di tutto.

La storia dell’infinito

Il concetto di infinito è da sempre uno dei motivi più affascinanti e d’ispirazione del pensiero matematico, spesso in relazione a diverse concezioni filosofiche e teoriche. Nell’antico mondo greco, per esempio, l’infinito si presenta con una grande varietà di aspetti che non sono solo matematici e filosofici, ma anche religiosi e persino poetici. Il termine infinito compare nella filosofia di Anassimandro: un filosofo presocratico ed il primo cartografo, che lo definì come una «materia infinita» all’origine di tutte le cose. Tuttavia, l’evoluzione del concetto di infinito fu ostacolata dai pitagorici, che orientarono il loro lavoro verso il finito ponendolo nella colonna del bene nella Tavola delle antitesi fondamentali e posizionando invece l’infinito in quella del male. Nella scuola di Elea invece, vennero presentati argomenti di carattere infinitesimale come il paradosso del piè veloce di Achille e della lenta tartaruga che lo sfidò ad una gara di corsa assicurandosi però un vantaggio iniziale, il quale però secondo l’antinomia non doveva essere mai raggiunto. Una prospettiva diversa invece fu proposta da Anassagora, il quale aiutato probabilmente dagli studi di prospettiva scenografica preannunciò: «Tanto nel grande quanto nel piccolo vi è lo stesso numero di particelle».

Aristotele invece distingueva tra infinito “potenziale” e “attuale”, descrivendo il primo fornendo l’esempio per cui per ogni numero naturale è possibile trovarne un successivo, e il secondo associandolo ai numeri naturali come tutti contemporaneamente esistenti. Anche Euclide, uno dei più grandi matematici di tutti i tempi, decise di seguire la linea aristotelica e di concentrarsi sull’infinito potenziale: per questo nella sua opera più famosa, gli Elementi, si parla di “segmenti infinitamente prolungabili” piuttosto che di rette. Tale avversione durò per secoli – tanto che nel Medioevo veniva riconosciuta l’esistenza di infiniti maggiori di altri ma ammettendo al contempo la legittimità dell’infinito attuale relegandolo ad esistente nella mente divina – fino allo sviluppo rinascimentale ed alla scuola di Galileo, che aiutata anche dall’apporto del mondo dell’arte e dai problemi di prospettiva predilige l’infinito attuale. Tuttavia, il vero e proprio cambio di marcia avvenne grazie all’opera di Georg Cantor, che lavorò alla definizione di insieme e dimostrò ufficialmente che esistono insiemi infiniti “più potenti” di altri insiemi anch’essi infiniti.

La gerarchia degli infiniti e gli insiemi numerici

Il primo insieme numerico infinito che viene insegnato sin da piccoli è quello dei numeri naturali, ovvero i numeri usati per contare e ordinare che partono da 0 e poi vanno ad 1, 2, 3 e così via. Poi vengono studiati i numeri interi (o relativi), che comprendono tutti i numeri naturali più i numeri negativi ottenuti ponendo il segno “-“ davanti ai naturali, come -1, -2, -3 e così via. Lo step successivo sono i numeri razionali, ovvero quelli ottenibili come rapporto tra due numeri interi primi tra loro, ovvero senza divisori comuni. Essi comprendono tutte le frazioni come 3/2, -2/5, 7/4 e così via, oltre che tutti i numeri precedentemente esposti. Infine, l’ultima generalizzazione riguarda i numeri reali, ovvero quelli che possono essere scritti con uno sviluppo decimale finito o infinito e che comprendono quindi tutti i razionali, le radici ed i numeri trascendenti, ovvero tutti quei numeri che non sono soluzione di nessuna equazione algebrica irriducibile a coefficienti interi (come il numero di Nepero “e” o il Pi greco “π”). Nonostante possa risultare intuitivo pensare che questi insiemi differiscano tutti tra loro per quanto riguarda la quantità di oggetti in essi contenuti (detta cardinalità), è possibile dimostrare che i primi tre, in realtà, contengono lo stesso numero di elementi, mentre il vero “salto” viene effettuato solamente quando si passa dai razionali ai reali.

Per prima cosa, è necessario stabilire un criterio che descriva quando due insiemi hanno lo stesso numero di elementi e questo, secondo l’assiomatica standard, avviene quando è possibile associare uno ad uno gli elementi tra il primo insieme ed il secondo. Per esempio, dato un insieme che contiene un astuccio, una penna ed un paio di forbici, è possibile dire che questo ha la stessa cardinalità di un insieme contenente una forchetta, un coltello ed un cucchiaio, perché è possibile associare o “accoppiare” l’astuccio alla forchetta, la penna al coltello e le forbici al cucchiaio (ovviamente l’ordine non conta e si sarebbe potuto associare l’astuccio al cucchiaio e così via). Per quanto riguarda i numeri naturali e quelli interi, è possibile definire un’associazione che accoppi lo 0 del primo insieme allo 0 del secondo, così come l’uno del primo insieme con l’uno del secondo, per poi associare il numero 2 al -1, il 3 al numero 2, il 4 al numero -2, il 5 al numero 3 e così via. Procedendo all’infinito, è possibile accorgersi che, nonostante i numeri interi sembrino il doppio dei naturali, ogni numero della prima famiglia avrà un numero naturale associato e quindi i due insiemi infiniti hanno in realtà la stessa “potenza” e quindi lo stesso numero di elementi. Da qui poi, il detto informale «infinito per due fa sempre infinito».

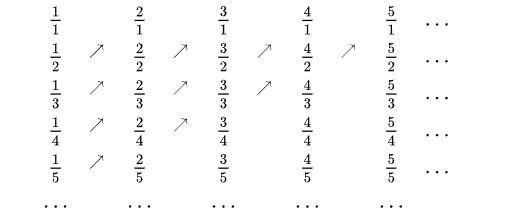
Per quanto riguarda i numeri razionali, la dimostrazione è meno intuitiva ma comunque ben posta. Cantor dispose i numeri razionali positivi in una tabella costruita in questo modo: nella prima riga ci sono tutti i numeri naturali espressi in frazione, ovvero 1/1, 2/1, 3/1 e così via, nella seconda riga tutti i numeri naturali divisi per due, ovvero 1/2, 2/2, 3/2 e così via, il che significa che la riga n-esima conterrà tutti i razionali costruiti dalla successione di naturali divisi per n, ovvero 1/n, 2/n, 3/n eccetera. Per costruire l’associazione, si può proseguire “scorrendo” la tabella per diagonali in direzione da sud-ovest a nord est, come nell’immagine che segue:

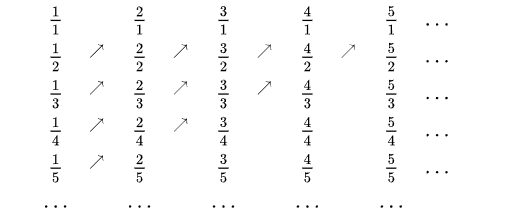
Se dalla lista ottenuta si cancellano poi le frazioni che si riferiscono in realtà allo stesso numero (come 1/1, 2/2, 3/3 che si riferiscono tutte al numero 1 o anche 4/2,8/4 e 18/9 che si riferiscono tutte al numero 2), si ottiene la successione 1, 1/2, 2, 1/3, 3, 1/4, 2/3, 3/2, 4 e così via, che può essere associata ai numeri naturali come segue, dimostrando quindi che l’insieme dei naturali e dei razionali possiedono lo stesso numero di elementi.

Per quanto riguarda i numeri reali invece, è possibile dimostrare che non solo non sono numerabili – ovvero con la cardinalità degli insiemi discussi precedentemente – ma che banalmente anche solo una loro piccola parte, come l’insieme dei numeri reali compresi nell’intervallo tra 0 e 1, non è numerabile. Per fare ciò Cantor sfrutta una tecnica chiamata “argomento diagonale”, ovvero suppone di scrivere tutti i numeri tra 0 e 1 in una tabella infinita che per esempio sarà formata da elementi del tipo:

r1 = 0,5105110…
r2 = 0,4132043…
r3 = 0,8245026…
r4 = 0,2330126…
…

E così via. Ora si supponga di costruire un nuovo numero considerando solo le cifre sulla diagonale, ovvero la prima cifra decimale del primo numero, la seconda del secondo e così via (quelle in grassetto). Avremo così, in questo esempio, il numero 0,5140… e, soprattutto, possiamo definirne un altro sommando ad ogni cifra il successivo (ovvero, in questo esempio, il numero 0,6251…). Tale numero, essendo compreso tra 0 e 1, dovrebbe per ipotesi essere compreso nella tabella infinita esposta precedentemente, ma ciò è assurdo perché significherebbe che tale numero all’interno della tabella dovrebbe essere uguale ad un altro che è stato costruito però cambiandogli una cifra. Da qui l’impossibilità di “numerare” i reali, da cui la dimostrazione del fatto che la cardinalità dei reali, detta “del continuo”, è superiore a quella degli insiemi numerabili quali i naturali, interi e razionali.

L’Ipotesi del continuo

La domanda che sorge spontanea ora, è chiedersi se esistano delle “vie di mezzo” tra i due, ovvero insiemi che sono “più potenti” dei numerabili ma che comunque presentano elementi in numero inferiore rispetto ai numeri reali che hanno la cardinalità del continuo. Tale dilemma si chiama Ipotesi del continuo (CH) e, nell’assiomatica standard che caratterizza la matematica che tutti conosciamo – chiamata assiomatica di Zermelo-Fraenkel – è stato dimostrato indecidibile, ovvero un enunciato che non può essere dimostrato né come vero né come falso. Nel 1940 infatti, Kurt Gödel dimostrò che l’Ipotesi del continuo non può essere dimostrata falsa, neppure con l’aggiunta dell’assioma della scelta, mentre nel 1963 Paul Cohen dimostrò che CH non può nemmeno essere dimostrata vera e che quindi l’enunciato è indipendente da tali assiomi. Tali scoperte innescarono una vera e propria divisione in correnti filosofiche che si chiesero se CH fosse stata risolta o meno, in che senso e che cos’è una soluzione. Tali dubbi si spinsero, e si spingono tutt’oggi, ad aree tutt’altro che intuitive e di facile comprensione, che includono il chiedersi se le conclusioni siano definitive o se è possibile che esistano scenari (magari con diversi assiomi di partenza) in cui l’Ipotesi sia vera e altri in cui sia falsa, se, come sostengono i platonisti, esista un’unica verità che dobbiamo ancora scoprire, oppure se esista un mix tra tutte le versioni precedenti, ammettendo un “multiverso” in cui esistono “mondi” dove CH è vera, altri dove è falsa e altri dove è indecidibile.

Cartesio, uno dei più grandi pensatori e filosofi di tutti i tempi, avvertiva di non affaticarsi troppo in discussioni riguardo all’infinito visto che, «dato che siamo finiti, sarebbe assurdo che noi stabilissimo alcunché su tale argomento e tentassimo in tal modo quasi di renderlo finito ed impadronircene». Tali considerazioni sembrano essersi concretizzate nel problema della risoluzione dell’Ipotesi del continuo, che sembra aver marcato i confini che delimitano fin dove può spingersi la comprensione umana, o almeno quella attuale. Nonostante l’incertezza riguardo ad ulteriori sviluppi teorici, nel frattempo è lecito congetturare che l’infinito, la teoria degli insiemi e quindi l’Ipotesi del continuo rimarranno una grandissima fonte d’ispirazione matematica e, al contempo, una delle aree di indagine più avvincenti della filosofia.

[di Roberto Demaio]